复习专题：幂函数

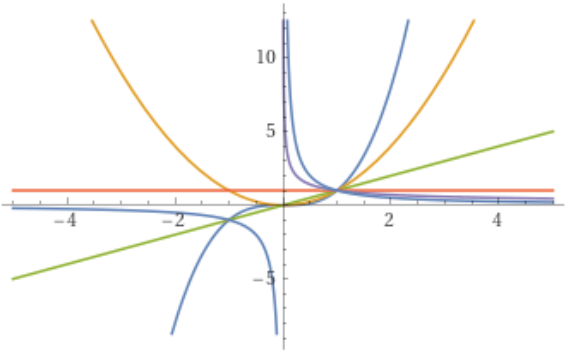
我上高中时没学过幂函数，所以这次复习相当于从头开始学。

一、幂函数的定义

幂函数：形如 $y=x^\alpha$ （$\alpha \in \mathbb{R}$）的函数叫作幂函数，其中 $\alpha$ 是常数，而且 $x$ 的系数是 1。

幂函数的指数 $\alpha$ 可以是正整数、正分数、0、负分数、负整数、无理数（高中阶段不讨论 $\alpha$ 为无理数的情形）。

二、必须掌握的幂函数

$y=x^3$，$y=x^2$，$y=x$，$y=x^\frac{1}{2}$，$y=x^0$，$y=x^{-1}$。

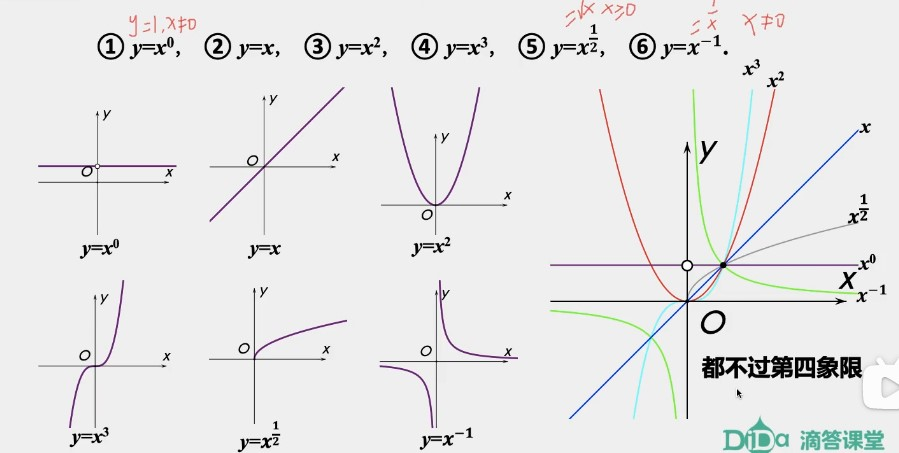
上述幂函数的共同性质：

1. 都不过第四象限。因为它们都是单值函数，一个 $x$ 只对应一个 $y$，既然过第一象限，就不会过第四象限。
2. 必过点 $(1,1)$。对于 $y=f(x)=x^\alpha$，总有 $y=f(1)=1^\alpha=1$。
3. $\alpha$ 对第一象限图像的影响。
   a. $a>1$，单增，曲线，快-立式
   b. $a=1$，单增，直线
   c. $0<a<1$，单增，曲线，慢-趴式
   d. $a=0$，没有单调性，与 $x$ 轴平行
   e. $a<0$，单减
   f. 当 $x>1$ 时，$\alpha$ 越大，函数 $x^\alpha$ 的图像（直线 $x=1$ 右侧的部分）越贴近直线 $x=1$；$\alpha$ 越小，函数 $x^\alpha$ 的图像越贴近 $x$ 轴。
   
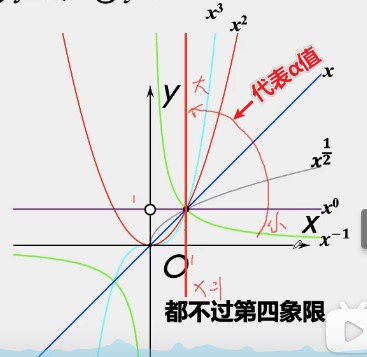
4. 当 $x>0$ 时，$y=x^\alpha$ 与 $y=x^\frac{1}{\alpha}$ 互为反函数（$\alpha \neq 0$），其图像在第一象限关于直线 $y=x$ 对称。

三、分类讨论幂函数的性质与图象

指数 $\alpha$ 会影响幂函数的性质和图象，所以我们需要根据 $\alpha$ 的取值进一步分类讨论。考试做题时，也是要这样分类讨论。

3.1 α 对定义域的影响

令 $y=x^{\alpha}=x^\frac{n}{m}$，其中 $\alpha,\ n,\ m>0$，而且 $\dfrac{n}{m}$ 是既约分数（无法再约分的分数）。如果 $\alpha$ 是整数，可看作 $n=\alpha,\ m=1$。

1. 原点。
   a. $\alpha>0$，定义域有 0，图象经过原点 $(0,0)$。
   b. $\alpha<0$，定义域没有 0，图象不经过原点。原因是 $x$ 在分母上。
   c. $\alpha=0$，定义域没有 0，图象不经过原点。原因是 $0^0$ 无意义。

2. 负数。($y=x^{\alpha}=x^\frac{n}{m}$)
   a. $m$ 为偶数，定义域无负数， 图象只经过第一象限。原因是开 $m$ 次方根，根号下不能为负数。
   b. $m$ 为奇数，定义域有负数， 图象经过 $y$ 轴左侧。原因是开 $m$ 次方根，根号下可以为奇数。

3.2 α 对第一象限单调性的影响

1. $\alpha=0$ ，无单调性，与坐标轴无交点。
2. $\alpha>0$，单增，经过原点。
   a. $\alpha>1$，曲线，单增，快，立式
   b. $\alpha=1$，直线 $y=x$，单增
   c. $0<\alpha<1$，曲线，单增，慢，趴式
3. $\alpha<0$，单减，与坐标轴无交点。

3.3 α 对奇偶性的影响

令 $y=x^{\alpha}=x^\frac{n}{m}$，其中 $\alpha,\ n,\ m>0$，而且 $\dfrac{n}{m}$ 是既约分数（无法再约分的分数）。如果 $\alpha$ 是整数，可看作 $n=\alpha,\ m=1$。

1. $m$ 和 $n$ 都为奇数，则幂函数为奇函数。原因是 $x$ 要乘以奇数次幂再开奇数次方根，$x$ 的符号不变，导致 $f(-x)=-f(x)$。
2. $m$ 为奇数，$n$ 为偶数，则幂函数 $y$ 为偶函数。原因是 $x$ 要乘以偶数次幂再开奇数次方根，导致 $f(-x)=f(x)$。
3. $m$ 为偶数，则幂函数 $y$ 为非奇非偶函数。原因是函数图像只经过第一象限。

幂函数整体的单调性，要由第一象限单调性和奇偶性共同决定（除非它只取到第一象限）。

四、一般幂函数图像的画法

1. 先根据指数 $\alpha$ 判断第一象限单调性，
2. 再根据指数 $\alpha$ 判断函数的定义域，能不能取到 0 或负数。
3. 再根据指数 $\alpha=\frac{n}{m}$ 判断函数的奇偶性，根据奇偶性补全函数的另一半。

五、幂函数大小的比较

5.1 比较大小

1. 指数相同，底数不同，利用幂函数单调性比较大小。

2. 底数相同，指数不同，利用指数函数单调性比较大小。

3. 如果指数、底数都不相同，我们可以化为指数相同、化为底数相同、找中间量、画图。

5.2 求解不等式 $f(x)^\alpha<g(x)^\alpha$ 的基本思路

利用幂函数 $y=x^\alpha$ 的性质转化为关于 $f(x)$ 和 $g(x)$ 的不等式（组）求解。

图片版权

题图： 用 WolframAlpha 绘制

头图：https://pixabay.com/zh/photos/munich-olympic-stadium-tv-tower-2516492/

文中截图如果没有特别注明，都是来自“滴答课堂”