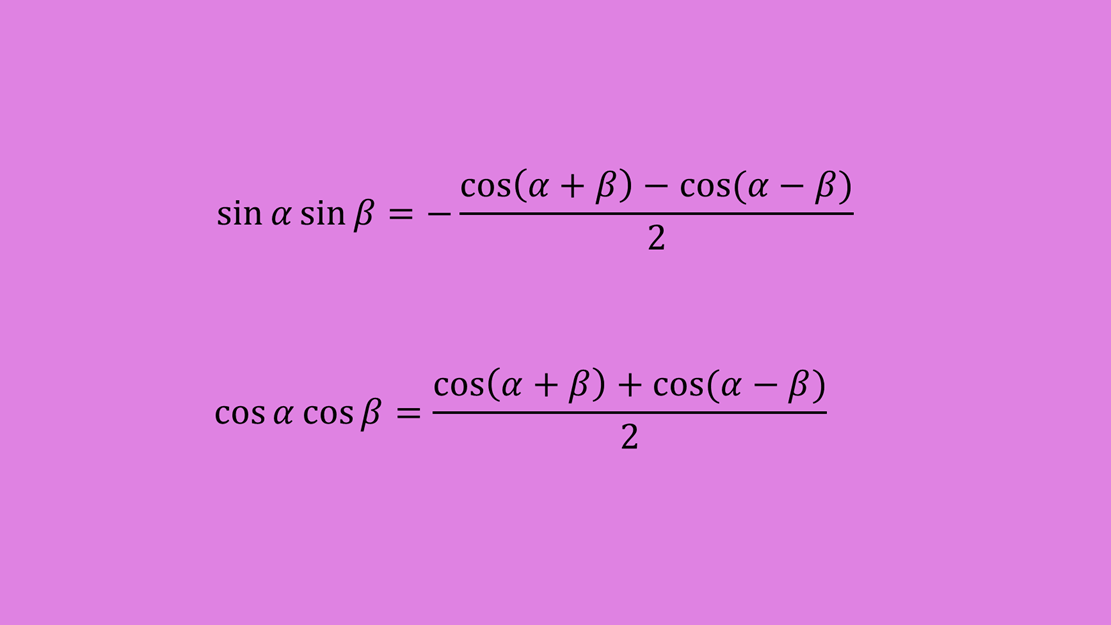本文最后更新于 2023-09-09T12:42:38+08:00
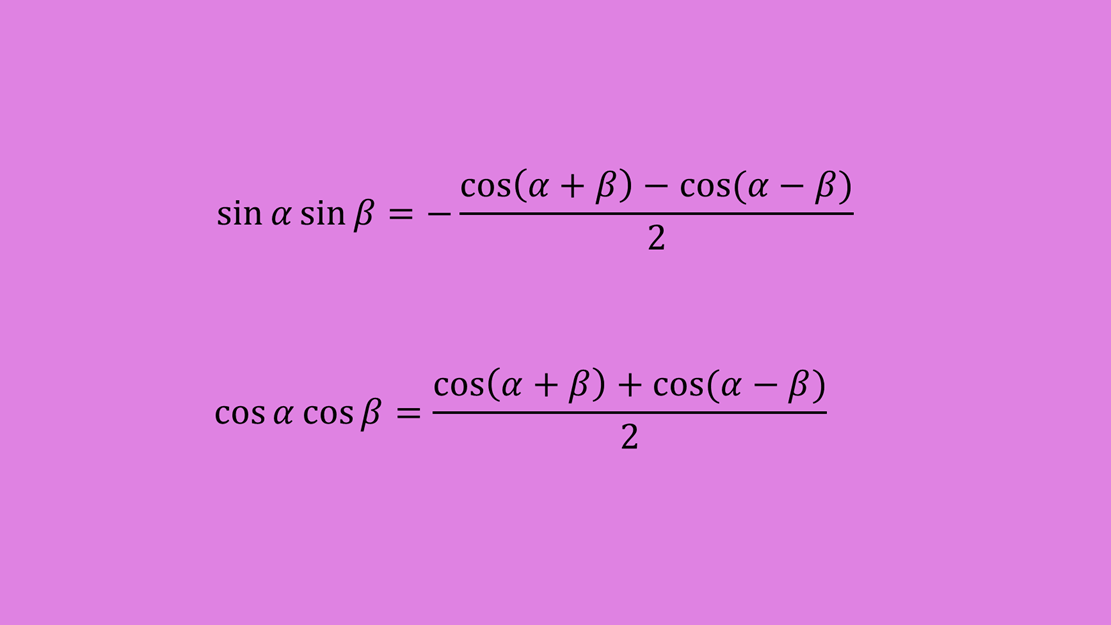
已知 0<β<α<2π,且 cos(α+β)=54,sin(α−β)=135,那么 cos2α=( )
A. 6563 B. −6563 C. 6533 D. 6556 或 −6516
【分析】 首先分析题干与待求问题之间的联系,容易看出 2α=(α+β)+(α−β)。那么我们怎样才能让 cos(α+β) 和 sin(α−β) 函数括号里的角相加?可以考虑 积化和差公式。
sin(α+β)sin(α−β)=−2cos2α−cos2β
cos(α+β)cos(α−β)=2cos2α+cos2β
这样,我们还得根据题给条件把 sin(α+β) 和 cos(α−β) 求出来,代入上述两式,就可以解得 cos2α了。
【解】 令 x=α+β,y=α−β
则有 x+y=2α,x−y=2β
因为 0<β<α<2π 而且 cosx>0,所以 0<x<2π
又因为 siny>0,所以 0<y<2π
由三角函数平方关系式,
sinx=1−cos2x=53
cosy=1−sin2y=1312
由积化和差公式,
sinxsiny=−2cos(x+y)−cos(x−y)=6515
cosxcosy=2cos(x+y)+cos(x−y)=6548
联立上述两式,消去 cos(x−y) ,解得 cos(x+y)=cos2α=6533
图片版权:
题图:自制。
头图:Image by peritas from Pixabay